Tutorial: cómo resolver puzzles lógicos

Los puzzles lógicos o de rejilla son acertijos en los que se nos da un pequeño contexto y se nos pide que determinemos algunas relaciones entre diferentes elementos como, por ejemplo, "determina quién vive en cada casa y qué mascota tiene".

Para ello, contamos con distintas categorías (nombre, color, disfraz, edad, etc.) y varios elementos de cada categoría (por ejemplo, dentro de "color", las posibilidades que nos dan son azul, verde, rojo y amarillo). El objetivo es relacionar cada uno de esos elementos con otro de cada una de las demás categorías (por ejemplo, a Pedro le gusta el color verde, va disfrazado de vampiro y tiene 9 años). Ningún elemento puede repetirse y todos tienen que ser usados. Además, en este tipo de acertijos siempre hay varias pistas, como "El niño que va de duende es más pequeño que el niño al que le gusta el color azul", que nos ayudan a descubrir la solución.

Uno de los puzzles lógicos más famosos, y que quizás conozcas, es el llamado "acertijo de Einstein" (aunque no está del todo claro quién fue su creador). En teoría, es un acertijo bastante complicado, ya que están involucradas un montón de categorías con sus respectivos elementos, pero eso es porque normalmente la gente lo intenta resolver sin utilizar una rejilla como ahora explicaré. Si te apetece intentarlo, aquí tienes más información sobre él (aunque ya adelanto que podrás verlo en el blog en un futuro). Como digo, si se resuelve de la manera general que ahora veremos, únicamente tiene una complicación: dibujar una rejilla muy grande.

Lo primero de todo para resolver un acertijo de este tipo es construir una rejilla, que es una cuadrícula que resume toda la información del problema. Al principio, estará vacía, pero poco a poco la iremos rellenando con cruces y círculos hasta que quede algo similar a esto:

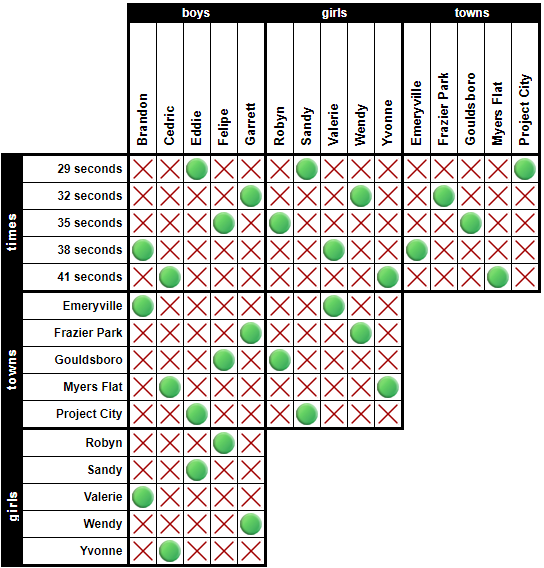
Lo que hacemos para construirla es: 1º- Identificar las categorías del acertijo, 2º- Identificar todos los elementos de cada categoría, 3º- Elegir una de las categorías (da igual cuál, se suele elegir alguna de las más importantes) y escribir sus elementos uno debajo del otro (en la imagen de arriba, es la categoría "times" con sus elementos "29 seconds", "32 seconds", etc.), 4º- Escribir el resto de categorías (de nuevo, el orden da igual) con sus elementos de forma que cada uno intersecte con los que ya habíamos colocado ("boys", "girls" y "towns" en la imagen, con sus elementos en vertical) y 5º- Escribir todas las categorías que hemos puesto en el anterior paso, excepto la primera, debajo de la que pusimos en el paso 3ª, pero en orden inverso. De esta forma, tenemos relacionadas cada una de las categorías con todas las demás. Observa que la mitad inferior derecha de la rejilla está vacía. Esto es porque no nos aportaría nada de información relacionar una categoría consigo misma o volver a relacionar dos que ya lo están en la otra mitad.

Y, ahora sí, vamos a ver un tutorial paso a paso de cómo resolver un puzzle lógico. Utilizaremos el que publiqué ayer y que creé para un concurso hace varios años. Tenemos que deducir en qué habitación se aloja cada uno de los 6 huéspedes y cuál fue su orden de llegada. Las pistas que nos dan son:

1- La señora Boyle llegó justo después del señor Wren.

2- El ocupante de la habitación verde llegó más tarde que el de la habitación azul.

3- Trotter no ocupa la habitación oeste ni la de roble, que la ocupa el que llegó en segundo lugar.

4- Metcalf llegó después que señor Wren pero antes que la señorita Casewell, que ocupa la habitación este.

5- El sargento Trotter llegó justo después de Paravicini.

6- El ocupante de la habitación azul no es Paravicini, que llegó después de Casewell.

7- El ocupante de la habitación rosa llegó el primero.

8- El que llegó en quinto lugar ocupa la habitación oeste, pero no es la señora Boyle.

Lo primero es lo primero: para construir la rejilla, identificamos primero las categorías y sus elementos:

Orden: 1, 2, 3, 4, 5, 6.
Nombre: Boyle, Wren, Trotter, Metcalf, Paravicini, Casewell.
Habitación: verde, azul, oeste, roble, este, rosa.

La rejilla queda así:

Comencemos a usar las pistas. La número 1 nos dice que "La señora Boyle llegó justo después del señor Wren". Por lo tanto, la señora Boyle no pudo ser la primera en llegar, ¿no? Y el señor Wren tampoco pudo ser el último. Como sabemos que esos dos casos son incorrectos: los tachamos con una cruz en nuestra rejilla:

Por ahora, esta pista no nos da más información, pero es posible que la necesitemos más adelante, así que la guardamos. La número 2 es "El ocupante de la habitación verde llegó más tarde que el de la habitación azul". Podemos usar un argumento idéntico al anterior y colocar dos cruces más:

De nuevo, todavía no hemos usado todo el potencial de esta pista, así que nos la guardamos para después. La número 3 es "Trotter no ocupa la habitación oeste ni la de roble, que la ocupa el que llegó en segundo lugar". Aquí se nos da tres piezas de información: que Trotter no está en la habitación oeste, que Trotter no está en la habitación de roble y que el segundo en llegar está en la de roble. Ponemos otras dos cruces para los dos primeros datos y, para el último, colocamos un círculo verde en la cuadrícula, que simboliza la relación correcta entre esos elementos (y, por lo tanto, podemos tachar todos los demás de la fila y columna):

Esta pista ya no nos podrá decir nada nuevo aparte de lo que ya tenemos, así que podemos descartarla. La número 4 es "Metcalf llegó después que señor Wren pero antes que la señorita Casewell, que ocupa la habitación este". De aquí, deducimos que Metcalf no es ni el primero en llegar ni el último, que el señor Wren no es ni el último ni el penúltimo, que la señorita Casewell no es ni la primera ni la segunda y que la señorita Casewell está en la habitación este:

Esta pista todavía puede sernos útil, la guardamos para más adelante. La número 5 es "El sargento Trotter llegó justo después de Paravicini". Similar a alguna de las pistas anteriores:

De nuevo, todavía podemos usar esta pista. La número 6 es "El ocupante de la habitación azul no es Paravicini, que llegó después de Casewell":

¡Mira! Ya podemos determinar quién llegó en primer lugar: el señor Wren.

La pista 7 es "El ocupante de la habitación rosa llegó el primero". Por lo tanto, Wren está en la habitación rosa:

Y la pista 8 es "El que llegó en quinto lugar ocupa la habitación oeste, pero no es la señora Boyle". Anotamos estos datos en nuestra rejilla:

Ya hemos terminado una primera ronda examinando una a una las pistas y hemos encontrado mucha información. Ahora, volvemos a revisar las pistas que no hemos descartado, para ver si, con los nuevos datos, nos ayudan más. Por ejemplo, de la número 1, que era "La señora Boyle llegó justo después del señor Wren", deducimos que Boyle llegó en segundo lugar, ya que ahora sabemos que Wren llegó el primero.

Pero también sabíamos que la segunda persona en llegar se aloja en la habitación de roble. Y, además, podemos determinar quién llegó en sexto lugar: Trotter. Y usando este último dato, podemos mezclar la información de la columna de Trotter con la de la fila del sexto lugar, lo que nos deja como única posibilidad la habitación verde:

En la parte inferior, podemos resolver un par de cosas:

Dado que Paravicini está en la habitación oeste y el que está en la habitación oeste llegó en quinto lugar... deducimos que Paravicini llegó en quinto lugar:

Volviendo a leer la pista número 4, "Metcalf llegó después que señor Wren pero antes que la señorita Casewell, que ocupa la habitación este", tenemos que Metacalf llegó antes que Casewell, lo que nos permite terminar de rellenar todo.

Por lo tanto, la solución es:

Wren llegó el primero y se aloja en la habitación rosa; la segunda en llegar fue la señora Boyle y estará en la habitación de roble; Metcalf llegó el tercero y dormirá en la habitación azul; en cuarto lugar llegó la señorita Casewell, que se hospeda en la habitación este; el señor Paravicini, que ocupa la habitación oeste, llegó el quinto; y, en sexto y último lugar, llegó el sargento Trotter, que se instalará en la habitación verde.

Y, con esto, termina el tutorial. ¡Ahora ya puedes resolver cualquier puzzle lógico!