Tutorial: cómo resolver nonogramas

Los nonogramas son un tipo de puzzles japoneses basados en la lógica cuyo objetivo es pintar una cuadrícula en blanco y negro y revelar un dibujo secreto. Para ello, se rellenan las casillas de negro o se dejan en blanco atendiendo a algunas pistas en el exterior de la cuadrícula.

En la siguiente imagen puedes ver un ejemplo de nonograma resuelto:

El punto de partida es una cuadrícula vacía con algunos números a la izquierda de cada fila y encima de cada columna. Estos números representan longitudes de secuencias continuas de casillas en negro que nos iríamos encontrando si fueramos recorriendo la fila/columna correspondiente. Por ejemplo, observa este otro nonograma resuelto:

La primera fila contiene una secuencia de 2 casillas negras seguidas; la segunda y tercera filas, una de 3; la cuarta, una secuencia de 3 y otra de 1 (en el mismo orden que los números de la izquierda).

El reto consiste en, conociendo esas longitudes de las secuencias, saber dónde colocarlas exactamente. Veamos un ejemplo paso a paso...

Tenemos una cuadrícula 10x13 por rellenar. Si te fijas, una de las pistas horizontales es un 13, lo que quiere decir que debemos pintar toda la fila:

Fíjate en la segunda columna, la que tiene un 6. En algún lugar de esta columna hay una secuencia de 6 casillas negras, pero no sabemos dónde. Si observamos los dos casos extremos:

y

Podemos observar que, estén donde estén, hay varias que siempre serán negras. Y este razonamiento puede aplicarse a la penúltima columna también:

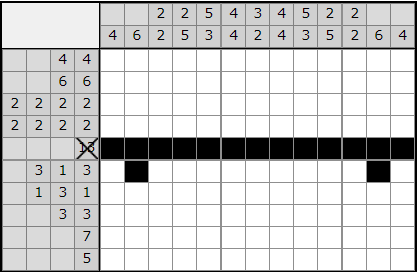
Podemos seguir una lógica parecida para la primera columna: tenemos que poner un segmento de 4 casillas y ya tenemos una colocada. Los dos casos extremos son:

y

En este caso, no podemos ver ninguna casilla que sea siempre negra. Pero podemos encontrar algunas que son siempre blancas. Y, de nuevo, este mismo razonamiento puede aplicarse a la última columna:

Lo que hemos estado haciendo hasta ahora es la táctica básica para resolver nonogramas. Probemos con la penúltima fila. ¿Dónde podría ir la secuencia de 7 casillas negras? Los dos casos extremos son:

y

Y, de ello, concluimos:

Nuestro siguiente paso será considerar las dos columnas centrales con dos segmentos de 4 casillas. Para el segmento de abajo, dado que la penúltima casilla la acabamos de pintar, las dos justo encima tienen que ser negras (independientemente de si la última casilla de la columna es negra o no).

No dejemos todavía estas columnas. Si la casilla que está por en medio fuera negra, tendríamos segmentos de 5 ó más casillas, y eso no puede ser. Por lo tanto, tiene que ser blanca. Y, por lo tanto, hemos encontrado dónde acaba el segmento de arriba y podemos reconstruirlo.

Mirando la columna central, vemos que algunas casillas nunca podrán ser negras, puesto que las secuencias no son lo suficientemente largas:

En la primera fila, los espacios que nos quedan son precisamente los que tenemos que pintar, no hay ninguna otra posibilidad:

Después de este último paso, tenemos bastante información sobre puntos donde comienzan secuencias:

Continuamos con las filas 2, 3 y 4:

Y, nuevamente, tenemos más información para completar algunas columnas:

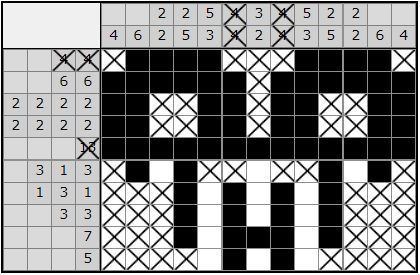
El siguiente paso es trivial:

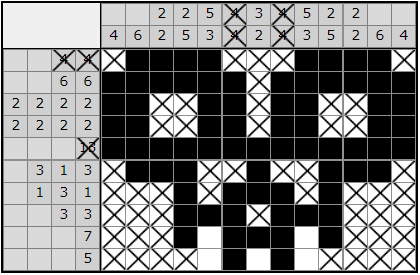
Y por fin llegamos a la solución del nonograma:

¿Te ha gustado resolver un nonograma? ¿Por qué no practicas con este otro? Es un poquito más grande, pero no deberías tener ningún problema. Para resolverlo, puedes utilizar un editor de imagen o imprimirlo, lo que prefieras.

Para ver la solución, pulsa el botón.

Y, con esto, termina el tutorial. ¡Ahora ya puedes resolver cualquier nonograma! ¿Por qué no pruebas los que están publicados en el blog? Puedes verlos AQUÍ.