Resuelve la siguiente pirámide numérica en la que cada número es la suma de los dos inmediatamente inferiores. Todos los números son enteros positivos.
Una vez que lo hayas resuelto, ¿qué particularidad tiene esta pirámide?
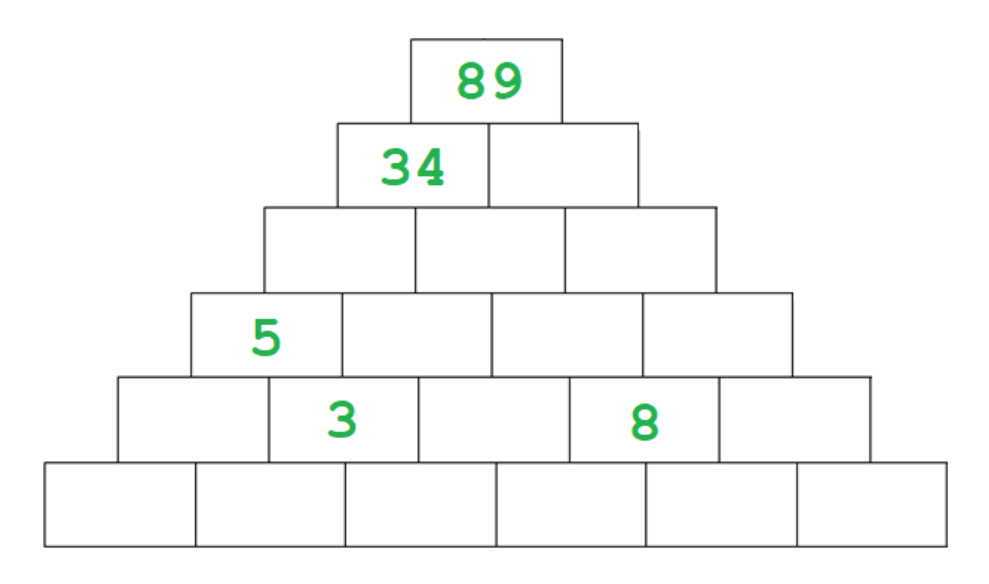
SOLUCIÓN: podemos poner inmediatamente un 55 que, sumado al 34, da como resultado el 89 de la cúspide; y un 2 que, sumado al 3, da el 5. Aparentemente, ya no podemos poner ningún otro número de forma obvia.
Pero, recordemos, todos son positivos y enteros, por lo que... ¿qué dos números podrían sumar 2? Sólo hay una posibilidad: 1 y 1. Con el segundo 1, encontramos un 2 para sumar 3.
Así, nos quedan tres huecos en la fila inferior. Llamaremos al primero con la incógnita "a". El segundo tiene que ser 8-a. Ahora, iremos subiendo por la pirámide calculando los valores en función de a.
En la segunda fila, el primer hueco tiene que valer a+2. En la tercera fila, los dos primeros lugares que están vacíos valen a+5 y a+10, por lo que los dos primeros huecos de la cuarta fila son a+10 y 2a+15. Estos dos números deben sumar 34: (a+10)+(2a+15) = 34, es decir, 3a+25 = 34 y obtenemos el valor de a=3. Podemos sustituirlo en todos los huecos que hemos utilizado hasta ahora.
Nos queda encontrar los valores del lateral derecho. De forma similar a como hicimos antes, llamamos "b" al valor inferior y vamos subiendo.
Los valores que encontramos en el camino son 5+b, 13+b y 26+b. Dado que 21 y 26+b tienen que sumar 55, 21+(26+b) = 55, es decir, 47+b = 55, por lo que b=8. Con este último dato, podemos terminar de rellenar la pirámide.

La particularidad que tiene esta pirámide numérica es que todos sus números son números de Fibonacci, por lo que en cada fila se repite la anterior corrida dos posiciones hacia la izquierda y se añade el siguiente de la serie al final.
No hay comentarios:
Publicar un comentario